przedziały Basia: Witaj Bogdanie Twój sposób oznaczania przedziałów jest naprawdę znakomity. Uważam, że powinieneś opublikować go w jakimś czasopiśmie, biuletynie lub przedstawić na jakimś innym szerokim forum zajmującym się metodyką nauczania matematyki (istnieje chyba coś takiego ?), bo jest wart upublicznienia i na pewno ułatwiłby życie całym pokoleniom uczniów i nauczycieli. Tym bardziej, że, moim zdaniem, nie można tej metodzie niczego zarzucić. Nie widzę w niej żadnych nieścisłości, ani żadnych innych "grzechów" przeciwko logice, jednoznaczności itp. Oczywiście trzeba się przyzwyczaić, ale to już niewielki kłopot. Gorąco Cię namawiam do upowszechnienia, nie tylko na forum. Pozdrawiam Basia

b.: podbijam

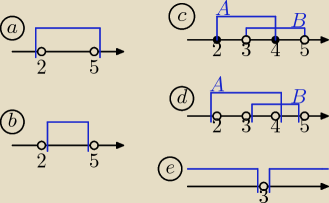
Bogdan: Dziękuję Basiu. Od wielu lat prezentuję oczywisty i naturalny sposób graficznego oznaczania przedziałów liczbowych. Podaję przykłady. Przedział obustronnie domknięty <2, 5> to przecież przedział zawierający w sobie skrajne punkty i to właśnie widać na rysunku (rysunek a,). Przedział obustronnie otwarty (2, 5) to przedział, w którym punkty 2 i 5 leżą poza przedziałem i są pierwszymi zewnętrznymi punktami przedziału (rys. b), co też wyraźnie widać na rysunku. Jak widać, nie ma potrzeby zamalowywania kółeczek i z tym właśnie zamalowywaniem walczę od dawna, ono wprowadza w błąd. Zamalowane kółeczko jest automatycznie brane jako domknięcie przedziału, szczególnie przy wyznaczaniu różnic przedziałów. Przykład: A = <2, 4>, B = (3, 5) Wyznaczyć A \ B, B \ A. Odczytując rozwiązanie z rysunku c (z zamalowanymi kółeczkami) często, a wiem to z wieloletniego doświadczenia, osoba rozwiązująca zapisuje taką odpowiedź: A \ B = <2, 3) B \ A = <4, 5). To są nieprawidłowe odpowiedzi. Błędów nie popełnia się biorąc rozwiązanie z rysunku d: A \ B = <2, 3> B \ A = (4, 5). Inny przykład: zbiór R\{3} można przedstawić graficznie w sposób pokazany na rys. e. Przyznam się, o ile że taki sposób oznaczania przedziałów jest przez uczniów przyjmowany jako pomoc i ułatwienie w rozwiązywaniu zadań, to przez nauczycieli jest raczej odrzucany. Można odnieść wrażenie, że uczący trzymają się kurczowo swoich nawyków i niechętnie przyjmują propozycje zmian.

Eta: Witam Ten sposób oznaczania przedziałów jest rewelacyjny ! Prosty, przejrzysty i powinien być stosowany przez wszystkich! Wreszcie skończyły się problemy z wytłumaczeniem (domkniętości, otwartości przedziałów) szczególnie przy wyznaczaniu różnicy przedziałów ( bo tu były największe problemy) Od dłuższego czasu .....dzięki Tobie Bogdanie zapomniałam o "głupich kółeczkach" rewelacja, rewelacja i jeszcze raz rewelacja ! Miłych snów , pozdrawiam

Jakub: Ciekawy sposób zapisu przedziałów. Dodałem komentarz o nim na stronie 7 z tradycyjnymi zapisami. Może się rozpowszechni.

xx: myślę, że osoby trochę więcej kumające matmę bez problemów odczytują kółeczka, a ci co tego nie potrafią zrozumieć to tych rysunków też by i nie zrobili i nie odczytali

Filip: Nie za bardzo rozumiem co jest takiego rewelacyjnego w tym nowym sposobie. Nie wiem w jaki sposób taki zapis ma być łatwiejszy od tradycyjnego. Zgadzam się z kolegą xx. Kto nie rozumiał kółeczek to i tego nie pojmie. Pozdrawiam.

Gustlik: Bogdan − sposób ciekawy! Dotychczas stosowałem sposób tradycyjny − z zamalowywaniem kółeczek. Rzeczywiście moi uczniowie przy odczytywaniu różnicy zbiorów mylili się w sposób taki, jaki Ty to opisałeś, niemniej znalazłem swój obrazowy sposób na wyeliminowanie tego błędu − wytłumaczyłem im, że przy wyznaczaniu róznicy zbiorów wynikowy przedział ma "na styku" z odejmowanym przedziałem odwrotny koniec do zaznaczonego, a więc jak "na styku" przedziałów jest kółeczko zamalowane, to wynik będzie miał kółeczko puste, a jak jest puste, to wynik będzie miał zamalowane. I to dotarło do uczniów.

misiekTSP: nic specjalnego, jak ktoś kumaty to zrozumie oba sposoby, z kolei jak ktoś ciemny to i z jednym i z drugim sposobem będzie miał problemy. "Odczytując rozwiązanie z rysunku c (z zamalowanymi kółeczkami) często, a wiem to z wieloletniego doświadczenia, osoba rozwiązująca zapisuje taką odpowiedź: A \ B = <2, 3) B \ A = <4, 5). " jak robią, aby szybciej, to może i tak wychodzi. jak się temu przyjrzeć logicznie, to od razu widać, że taka odpowiedź jest zła. jeśli ze zbioru A zabierzemy B(a 3 do B nie należy! w końcu dlatego kółko jest puste, to nam o czymś mówi), to A\B będzie kończyło się na 3 WŁĄCZNIE.

Gustlik: Co do nauczycieli − to masz rację. Nie dość, że kurzcowo trzymają się swoich nawyków, to jeszcze te nawyki to na ogół okrężne, czasochłonne i mało przejrzyste metody rozwiązywania zadań. Pozdrawiam.

dupa xd:

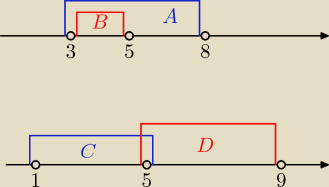
Gustlik: Bogdan, muszę Ci powiedzieć, że Twoja metoda zaznaczania przedziałów zrobiła fururę wśród moich uczniów. Wszystko WIDAĆ jak na dłoni. Metoda przydaje się jeszcze w takich sytuacjach: A=<3, 8) − rys. u góry B=(3, 5) Wyznacz A∩B Rozwiązując "tradycyjną" metodą wielu uczniów nie wiedziałoby, co zrobić z "3". A tu widać wszystko jak na dłoni, że będzie to (3, 5). Inny przykład − rys. u dołu: C=<1, 5> D=<5, 9) Wyznacz C∩D. Rozwiązując "tradycyjną" metodą wielu uczniów nie wiedziałoby, co zrobić z "5". A tu widać wszystko jak na dłoni, że będzie to {5}, czyli "sama 5" − zbiór jednoelementowy.

Gustlik: Oczywiście "furorę", sorry za literówkę.

MathGym: Nie wiem czym się tak ekscytujecie. Od niepamiętnych czasów używam takich oznaczeń, więc nie jest to żadna nowośc Pozdrawiam

Eta: I tak trzymaj ! Pozdrawiam

Karniacz: Karny.... dla matematyki !

dsds: Down

Gustlik: Ten karny to by sie przydał "TFUrcom" nowej podstawy programowej z MEN−u za totalne spapranie programu nauczania tego przedmiotu i wywalenie prostych wzorów i twierdzeń z poziomu podstawowego oraz nauczycielom z Bożej łaski stosującym metody "do Rzymu przez Krym".

Mati: ja zgodzę się z xx standardowa metoda oznaczania przedziałów dla ludzi którzy rozumieją matematykę nie będzie stanowić problemu, jeśli ktoś nie ma o tym pojęcia to z czasem zobaczycie że i ta metoda będzie się uczniom mylić, chociażby niedokładny rysunek, kreska za kółeczkiem czy przed... i całe zadanie zle

Joanna: m(×+1)−3m=×+2